Haskell で線形識別関数の学習を行う
これまでに作ってきた行列演算の応用として、パターン認識の分野での識別関数の学習処理を行う。
ここで言う学習とは、特徴空間においてクラスを分断する領域を推定する事である。
今回は識別関数の中でも、特徴空間において線形にクラスを分離する識別面の学習を行う。
下記の資料で、これについてわかりやすく解説している。以下のプログラムの内容は、同資料の p39 - 42 の内容になる。
http://www3.sys.es.osaka-u.ac.jp/iwai/slc/H16/01intro.pdf
資料だけでは分かりづらいので、p41 の内容を補足する。
資料にもあるように出力と教師信号の誤差の二乗なので、評価関数は ω の二次関数になっている。
誤差 (出力と教師信号の差) を最小にする識別面を取得したいので、評価関数の最小値を取得すればよい。資料にもあるように、評価関数は誤差の二次関数であり、誤差は ω の関数なので、
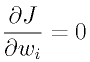 [1]
[1]
が評価関数 J の極小値になる。ここで w_i はクラス i におけるパラメータベクトルを表す。
また、クラス i における p 番目の入力を z_p としたとき
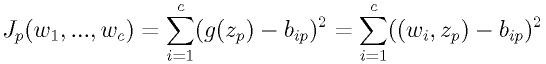 [2]
[2]
より
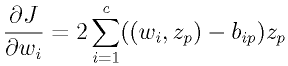 [3]
[3]
なので、あるクラス i の全ての入力に対する評価関数を最小にするパラメータを求めるには、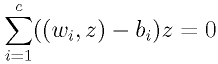 [4]
[4]
を満たす ω を各クラスについて求めればよい。
ここで Haskell プログラムについて見る前に、線形識別関数 g_i(z) について考える。
d 次元の入力 z における g_i(z) は
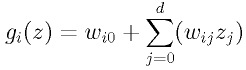 [5]
[5]
と考えられる。ここで w_{ij} (j = 1 ... j) は、識別面の法線ベクトルであり、w_{i0} は識別面 (境界) のバイアスになる。
ここで、d 次元ベクトルである z = (z_1, z_2, ... , z_d) を
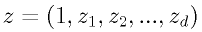 [6]
[6]
として (d + 1) 次元にする事で、上記の識別関数を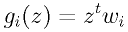 [7]
[7]
で表す。ここで、
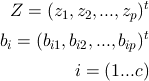
とする。なお、z_i (i=0 ... p) は 上記の (d + 1) 次元ベクトルを表すので、Z は p * (d+1) 行列となる。
ここで (4) よりあるクラス i に関して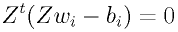 [8]
[8]
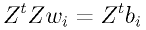 [9]
[9]
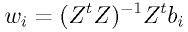 [10]
[10]
として、識別面の法線ベクトル w_i が求められる。
ここで作成した Haskell プログラムを見る。以下に、コード全体のリンクと、追加部分のコードを記載する。
ソースコード
getPrototype xs tv = let lMx = expandDimension xs
lMxt = transpose lMx
ilMx = inverseMatrix $ lMxt /**/ lMx
in (ilMx /**/ (toRatio lMxt)) /**/ (transpose $ map (\x -> map (\y -> (y%1)) x) tv)
expandDimension :: [[Int]] -> [[Int]]
expandDimension mx = map (\xs -> 1:xs) mx
ここでは一次元空間における 2 クラス問題について考え、クラス 1 に属する学習パターンを
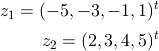
とし、教師ベクトルを
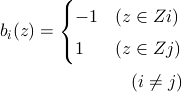
としている。
新たに作成した関数は 2 つだけである。
expandDimention 関数で入力パターン Z の次元の拡張をし、getPrototype 関数で、これまで作ってきた行列演算を行う関数を呼び出し、[10] 式を解いている。
出力結果は次のようになる。
[[(-115)%687],[184%687]]
つまり、学習した識別関数は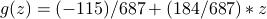
となる。グラフに出力すると次のようになる。
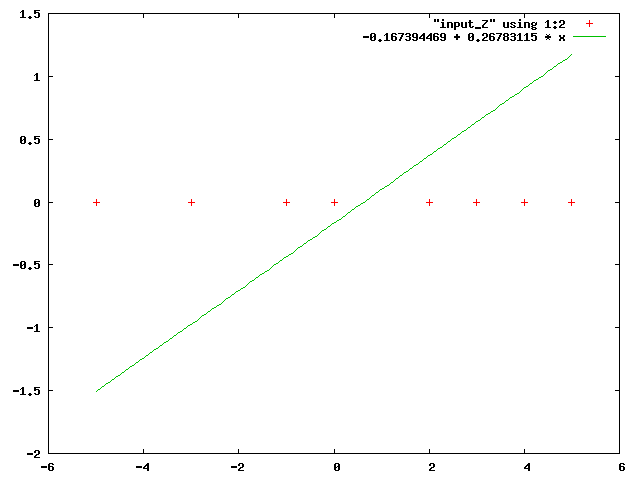
パターン出力の推定を行わない学習 (ノンパラメトリック学習) による識別関数の学習手法は他にも、パーセプトロンの学習規則や
Widrow-Hoff
の学習規則などの有名な手法が提案されているが。これら解析的に求める手法とは違い、ここでは評価関数を最小にするという観点から偏微分を行い、方程式を解くだけで識別面の学習が行えるという、非常にリーズナブルな手法である。
このの手法はとっても便利で、一見万能そうだが。[10] 式中の (Z^t Z) の逆行列が存在しなかったり、教師ベクトルを適切に設定しないと所望の識別面は得られない。
・おわりに
今回作成したプログラムの入力は 1 次元のリストだったが。 Haskell では行列演算のみ定義しているので、同一のプログラムで次元数をいくらでも増やすことができる。
- Category(s)
- 学習経過
- The URL to Trackback this entry is:
- http://dev.ariel-networks.com/Members/ohyama/haskell-7dda5f628b58522595a26570306e5b667fd23092884c3046/tbping