今回は DFT (discrete Fourier transform : 離散フーリエ変換) を使って、時間域の入力信号から周波数スペクトルに変換するプログラムを作成する。

 ソースコード

  プログラムの自体は、DFT の式をプログラムにするだけで簡単なので。その結果からどんな事が言えるのかといった考察について、今後忘れないように詳しく記載する。

  N 点の DFT による k 番目 (k = 0,1, ... , N-1) の出力は次のように得られる

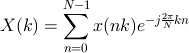
  x(nk) は正規化した (デジタル化した) 入力信号になり、j は虚数単位を表す。

  またオイラーの公式により



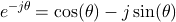
  が得られるので。サンプリング周波数を f としたとき、任意の信号 x を f を基本周期とする sin 波と cos 波の高調波に分解できる。
  ちなみに。何故わざわざ複素平面を使っているかというと、単にオイラーの公式が使いたいだけで、それ以外に意味は無い。

  さっそくやってみる。
  以下はコードの DFT 処理部分を抜粋したものになる。

dft :: [Double] -> [(Double,Double)]
dft sig = rdft 0 (length sig)
 where
  rdft :: Int -> Int -> [(Double,Double)]
  rdft i n | i == n = []
           | True = let rval = rdft' 0 i n
                        ival = idft' 0 i n
                    in (rval,ival):(rdft (i+1) n)

  rdft' j i n | j == n = 0
              | True = let val = head $ reverse $ take (j+1) sig
                       in (val * (cos ((2 * pi * (fromIntegral i) * (fromIntegral j))/(fromIntegral n)))) + (rdft' (j+1) i n) 

  idft' j i n | j == n = 0
              | True = let val = head $ reverse $ take (j+1) sig
                       in ((val * (sin ((2 * pi * (fromIntegral i) * (fromIntegral j))/(fromIntegral n))))*(-1)) + (idft' (j+1) i n) 

  ここに次の信号を 8 分割したものを 8 点 DFT で出力する。



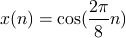
  出力結果

  [(0.0,0.0),(8.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(8.0,0.0)]

  k = 1, 7 でスペクトルが立ち、いづもれ (r, i) = (8, 0) となっている。
  つまり、入力信号は 8 点 DFT の枠の中に 1 周期の cos 波が 1 個入っている、という事がわかる。

  次に、これの半分の周期の sin 波を入れてみる。



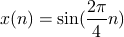
  出力結果

  [(0.0,0.0),(0.0,0.0),(0.0,-4.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,4.0),(0.0,0.0)]

  k = 2, 6 でスペクトルが立ち、k = 2 では (r, i) = (0, -4), k = 6 では (r, i) = (0, 4) となっている。
  ここで、k = 2 の符号が負になっている理由と、N/2 で結果が折り返されている理由について述べる。


 
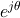
  は複素平面上での単位円を表しており、DFT はこの単位円上の (r, i) = (1, 0) からの時計回りのなす角の各周波数成分における sin と cos  の成分を抽出している。
  sin 波の周波数スペクトルが負になっているのと周波数スペクトルが N/2 で反転しているのは、8 点 DFT における k = 2 が角度 π / 2 を表しており、その時のオイラーの公式による sin 波成分の符号が負である為に、符号がマイナスになっている。同様の理由によって、k = 6 で符号が反転した絶対値が等しいスペクトルが得られる。
  また、スペクトルの絶対値は、(元の振幅 * n) / 2 となっている。この理由は、逆フーリエ変換をする事で理解できる。単なる計算だし、説明も長くなるので割愛する。

  最後に、上述の　2 つの信号の合成波を入れてみる。



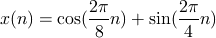
  出力結果

  [(0.0,0.0),(4.0,0.0),(0.0,-4.0),(0.0,0.0),(0.0,0.0),(0.0,0.0),(0.0,4.0),(4.0,0.0)]

  これによって。適切なサンプリング周波数を設定すれば、どんな複雑な音でも理論上 sin と cos に分割できる。

・終わりに
  これによって、入力信号 (例えば音声) を (sin 成分, cos 成分, 振幅) の三次元に分割する事が可能となった。

  え？ FFT ？ 大丈夫、わかってますよ。