資料の原稿
「詳説 正規表現」を読む、勉強会資料です。 プレゼン形式(S5)の表示 - http://dev.ariel-networks.com/articles/workshop/regex/paper/s5_document
教科書
- 「詳説 正規表現」 ISBN4-900900-45-1
- 参考書
- 「コンパイラ」(通称ドラゴンブック) ISBN4-7819-0585-4
- 「プログラミング作法」 ISBN4-7561-3649-4
目次
- 導入
- 正規表現の基本
- 正規表現の歴史(ひと休み)
- 正規表現の形式論
- 正規表現のマッチ
- NFA正規表現のメカニズム
- DFA正規表現のメカニズム
- NFA vs. DFA
導入
1. 導入
21世紀の今、正規表現を学ぶ意味
- 正規表現は現代のソフトウェアに残された魔法に見える技術のひとつだから
- 言語体系を積み上げるソフトウェア設計の理解に近づくから
正規表現とは
- 正確な定義や歴史は後ほど
- テキストのパターンマッチングや字句解析に便利な記法です
- 正確な定義より、例を見ながらの方が理解しやすいはずです
- 英語ではregular expression
- ファイル名展開のワイルドカード(*.txtなど)に似ていますが、違うものです
このプレゼンでのコマンド表記例
$ perl -ne 'ソース' 入力 出力
正規表現パターンがマッチ
パターン: cat
- テキスト: vacation
catの部分にマッチ
cf. キーワード検索
キーワード: cat
- テキスト: The cat takes a vacation.
catの単語にマッチ
正規表現の基本
2.正規表現の基本
メタ文字: ^と$
| ^(キャレット) | 行の先頭 |
| $(ダラー) | 行の末尾 |
- パターン: ^cat
- 行の先頭、リテラルc、リテラルa、リテラルtの連結
- パターン: cat$
- リテラルc、リテラルa、リテラルt、行の末尾の連結
- パターン: ^$
- 行の先頭、行の末尾の連結 (空行にマッチする)
メタ文字: 文字クラス
greyもしくはgrayにマッチさせたい。
- パターン: gr[ea]y
- リテラルg、リテラルr、リテラルe または リテラルa、リテラルyの連結
長くなるので特別な理由が無い限り、以下、リテラルxは単にxと表記します
メタ文字: 文字クラス(cont.)
「詳説 正規表現」 p10から引用
文字クラスは、それ自体が小さな言語であると考えてほしい。どのメタ文字がサポートされているかという規則(とその振舞い)は、文字クラスの内部と外部とで完全に異なる。
- パターン: [.$]
- リテラル.、リテラル$のいずれかの文字
メタ文字: 文字クラスの省略表記
- パターン: [0-9]
- 0,1,2,3,4,5,6,7,8,9のいずれかの文字
- パターン: [0-9A-Za-z]
- 数字、アルファベットのいずれかの文字
| -(ダッシュ) | 文字クラスの中でのみメタ文字。ただし先頭で使うと非メタ文字 |
- パターン: [-0-9]
- -,0,1,2,3,4,5,6,7,8,9のいずれかの文字
メタ文字: 否定文字クラス
- パターン: [^a]
- aで無い文字
- パターン: [^0-9]
- 0,1,2,3,4,5,6,7,8,9のどれでも無い文字
| ^(キャレット) | 文字クラスの先頭の場合はメタ文字。先頭以外で使うと非メタ文字 |
- パターン: [a^b]
- リテラルa、リテラル^、リテラルbのどれでも無い文字
メタ文字: 選択
- パターン: Subject|From
- 正規表現Subject または 正規表現From のいずれか
選択演算子 |(バー)の結合順位は低いので、通常丸カッコを併用する
greyもしくはgrayにマッチさせたい。
- パターン: gra|ey
- はダメ (gra または ey を意味するので)
- パターン: gr(a|e)y
- と書く必要があります。
メタ文字: 選択(cont.)
- パターン: ^Subject|From
- 正規表現^Subject または 正規表現From のいずれか
行頭のSubject または 行頭のFromにマッチさせたい場合は次のように書きます。
- パターン: ^(Subject|From)
- 行の先頭、Subject または From の連結
あるいは
- パターン: ^Subject|^From
- 行の先頭、Subjectの連結 または 行の先頭、Fromの連結
メタ文字: 繰り返しの後置演算子
| ? | 0回または1回の繰り返し後置演算子 |
| * | 0回以上の繰り返し後置演算子 |
| + | 1回以上の繰り返し後置演算子 |
| {n,m} | 最低n回、最大m回の繰り返し後置演算子 |
メタ文字: 繰り返しの後置演算子(cont.)
- パターン: colou?r
- c, o, l, o, u?, rの連結
- パターン: u?
- uが0回または1回
つまり、colorとcolourの両方にマッチ
丸カッコで後置演算子の範囲を指定できます。
- パターン: 4(th)?
- 4, (th)?の連結
4にも4thにもマッチ
*と+は「正規表現のマッチ」(後述)を参照
メタ文字: 丸カッコ
- 丸カッコで正規表現の部分パターンを記憶して前方参照ができます。
- 記憶した部分パターンは、\n(バックスラッシュと数字)で参照できます。
- パターン: ([0-9][0-9])x\1
- 数字二桁の部分パターン、リテラルx、一番目の部分パターンの連結
- 12x12: マッチ
- 89x89: マッチ
- 12x89: 非マッチ
- 12x1 : 非マッチ
- 1x1 : 非マッチ
メタ文字: 丸カッコ(cont.)
部分パターンのより高度な利用。
- 置換に利用
$ perl -ne 'if (s/([0-9][0-9])x([0-9][0-9])/\\2x\\1/) {print;}'
12x89
89x12
メタ文字: 丸カッコ(cont.2)
- 部分パターンの取り出し
$ perl -ne 'if (m/([0-9][0-9])x([0-9][0-9])/) {print "former is $1, latter is $2\\n";}'
12x89
former is 12, latter is 89
# 部分パターンの取り出し方はツール依存です。
メタ文字: 丸カッコ(cont.3)
丸カッコには独立した3つの用法があります。
- 選択の範囲指定 (Subject|From)
- 繰り返しの範囲指定 4(th)?
- 部分パターンの記憶
- 注意
- 1や2の用法でも部分パターンに記憶されます。
$ perl -ne 'if (m/^(Subject|From)/) {print "found $1\\n";}'
From: me
found From
メタ文字: エスケープ
メタ文字にリテラルとしてマッチさせたい場合、\(バックスラッシュ)でエスケープします。
- パターン: \.emacs\.el
- リテラル.(dot)、e、m、a、c、s、リテラル.(dot)、リテラルe、リテラルl の連結
- 注意
- ツール自体が持つエスケープ文字との混同に注意
便利かつサポートしているツールが多い文字クラスの省略表記
詳しくは「詳説 正規表現」p85もしくは各ツールのマニュアル参照。
| \w | 単語構成文字。多くの場合 [a-zA-Z0-9]または[a-zA-Z0-9\_] |
| \W | 非単語構成文字。\wを[^...]で反対の意味にしたもの |
| \s | 空白文字。多くの場合 [ \f\n\r\t\v] |
| \S | 非空白文字。\sを[^...]で反対の意味にしたもの |
| \d | 数字。多くの場合 [0-9] |
| \D | 非数字。多くの場合 [^0-9] |
POSIX
POSIX(Portable Operating System Interface)
http://www.opengroup.org/certification/posix-home.html
POSIX(R) Certified by IEEE and The Open Group
Although coined to refer to the original IEEE standard 1003.1-1988, today POSIX(R) refers to a family or set of IEEE and ISO standards
| BRE | Basic Regular Expressions |
| ERE | Extended Regular Expressions |
教養としてだけ正規表現を知りたいなら、POSIX規格の正規表現を学んでください。
知ったかぶり豆知識2
http://www.opengroup.org/austin/papers/posix_faq.html
The name POSIX was suggested by Richard Stallman. It is expected to be pronounced pahz-icks, as in positive, not poh-six, or other variations.
- 超意訳
- "POSIX"は、心の中でありがとうストールマン先生と言いながら、ポー!ジックスと呼びましょう。
3. 正規表現の歴史(ひと休み)
3. 正規表現の歴史(ひと休み)
正規表現の歴史
「詳説 正規表現」p66
- 1940年代初頭 神経生理学者がニューロンのモデル化
- 数年後 数学者Stephan Kleeneが代数モデルで記述。regular setsと呼ぶ
- 1950年代1960年代 理論数学者による研究
- 1968年 Ken Thompsonの論文「Regular Expression Search Algorithm」
- エディタqed (edの原型らしい)
- エディタed (今でも現役!)
- edのコマンド g/Regular Expression/p (Global Regular Expression Print)
- grep誕生
- egrep誕生 (Alfred Aho(ドラゴンブックの著者のひとり。awkのa)。DFA版grep)
- 1986年 Henry Spencerが(当時では初めて)自由に使えるC言語版の正規表現パッケージを開発
4. 正規表現の形式論
正規表現の形式論
言語に対する演算
「ドラゴンブック」 p110-112
| 演算 | 表記 | 定義 |
|---|---|---|
| LとMとの集合和 | L∪M | L∪M = {s|sはLまたはMの要素} |
| LとMとの連結 | LM | LM = {st|sはLの要素であり、tはMの要素} |
| Lのクリーネ閉包 | L* | Lの0回以上の出現 |
| Lの正の閉包 | L+ | Lの1回以上の出現 |
正規表現の定義
表記の前提: 正規表現rで表される言語(=記号列の集合)をL(r)と呼ぶことにします。
- {ε}(空の集合)は正規表現
- 記号aに対して、{a}(=記号列aだけの集合)は正規表現
- rとsが正規表現で、それぞれが表す言語をL(r)、L(s)とする。
- (r)|(s)は L(r)∪L(s)を表す正規表現
- (r)(s)はL(r)L(s)を表す正規表現
- (r)*は(L(r))*を表す正規表現
- (r)はL(r)を表す正規表現
正規表現が表す言語を正規集合と呼びます。
演算子
- 単項演算子*は、順位がもっとも高く、左結合
- 連結は、*の次順位が高く、左結合
- |は順位がもっとも低く、左結合
演算子の省略記法
- 1回以上の繰り返しは後置演算子+を用いる。
演算子+の順位は演算子*と同じ。
- r* = r+|ε
- r+ = rr*
- 0回か1回かの出現には後置演算子?を用いる。
- r? = r|ε
- 文字クラス[abc]は正規表現 a|b|c を表す。
知ったかぶり豆知識3
「ドラゴンブック」p206
- かっこの釣合のとれた構造は文脈自由文法なら記述できます。
- また、正規表現で記述できる構文はかならず文脈自由文法で記述できます。
Q. 「なぜ字句解析は正規表現(lexの世界)で行い、構文解析は文脈自由文法(yaccの世界)なのか?」
A. 「正規表現の方が簡単だから」
5. 正規表現のマッチ
正規表現のマッチ
マッチの原則
- 最初のマッチが優先 (最左)
- 繰り返し制御は欲張り(greedy)
- 例を見ながら身体で覚えます。
- NFAの実装イメージを頭の中に持つのが一番良いかもしれません(後述)。
- 「最左最長」という言葉だけ覚えても、たぶん使えません。
マッチの問題1: 解答
$ echo toatob | perl -ne 'if (m/to(b?)/) {print "found $1\\n";}'
found
全体がマッチしますが、(b?)は部分マッチしません。
脳内正規表現エンジン
- リテラルt、リテラルoがtoにマッチ
- b?は0回の繰り返しでマッチ
もっと良さそうに見える最後の tob にはマッチしません。
マッチの問題2: 解答
$ perl -ne 'if (m/^.*([0-9][0-9])/) {print "found $1\\n";}'
abc1abc23abc45xyz
found 45
脳内正規表現エンジン
- ^が行頭でマッチ
- .*が最後のzまでマッチ
- バックトラックして[0-9][0-9]にマッチする文字列を検索 => 45に部分マッチ
マッチの問題3: 解答
$ perl -ne 'if (m/^.*([0-9][0-9])?/) {print "found $1\\n";}'
abc1abc23abc45xyz
found
(パターンはマッチしますが、丸カッコの部分マッチは無し)
脳内正規表現エンジン
- ^が行頭でマッチ
- .*が最後のzまでマッチして終わり
greedyな繰り返しのありがちな例(cont.)
$ perl -ne 'if (m/"(.*)"/) {print "found $1\\n";}'
"it looks working"
found it looks working
"am i good at perl?". "NO"
found "am i good at perl?". "NO" <===これは意図とは違うはず
greedyな繰り返しのありがちな例(cont.2)
常套手段のパターン: "([^"]*)"
$ perl -ne 'if (m/"([^"]*)"/) {print "found $1\\n";}'
"it looks working"
found it looks working
"am i good at perl?". "NO"
found am i good at perl? <===この場合は意図通り
マッチ成立はマッチ不成立より優先(cont.)
$ perl -ne 'if (m/(\\.\\d\\d[1-9]?)\\d+/) {print "found $1\\n";}'
27.625
found .62
脳内正規表現エンジン
- \.(ドットリテラル)がマッチ
- \d(数字文字クラス)が6にマッチ
- \d(数字文字クラス)が2にマッチ
- [1-9]?が5にマッチ (マッチさせなくても全体はマッチする)
- \d+でバックトラックして5を奪ってマッチ (全体のマッチを優先)
選択はgreedy?
微妙。
正規表現のエンジンによって結果が異なります。
$ echo tonight | perl -ne 'if (m/to(ni|night)/) {print "found $1\\n";}'
found ni
$ echo tonight | perl -ne 'if (m/to(night|ni)/) {print "found $1\\n";}'
found night
Perl(従来型NFA)だとgreedyではありません。
DFAやPOSIX NFAでは上のどちらの場合でも night が部分マッチします。
マッチ色々、人生色々
$ echo tonight | perl -ne 'if (m/to(ni)*(ght)*/) {print "found $1, $2\\n";}'
found ni, ght
$ echo tonight | perl -ne 'if (m/to(ni)*(night)*/) {print "found $1, $2\\n";}'
found ni,
$ echo tonight | perl -ne 'if (m/to(ni)*(night)+/) {print "found $1, $2\\n";}'
found , night
6. NFA正規表現のメカニズム
NFA正規表現のメカニズム
NFA正規表現エンジン
- NFA(Nondeterministic Finite Automaton)
- 非決定性有限オートマトン
バックトラックが肝。 簡易な実装例を見るのが一番分かりやすい。
NFAの形式論はDFAの説明と一緒に行います。
NFA正規表現サブセットの実装例
「プログラミング作法」 第9章 記法 の例を更に簡略化
/* textからregexpを検索
* サポートするメタ文字: .と* の2つのみ、*は直前の1文字の0回以上の繰り返し */
int match(const char *regexp, const char *text)
{
do {
if (matchhere(regexp, text)) {
return 1;
}
} while (*text++ != '\\0');
return 0;
}
NFA正規表現サブセットの実装例(cont.)
/* textの先頭にあるregexpを検索 */
int matchhere(const char *regexp, const char *text)
{
if (regexp[0] == '\0') {
return 1;
}
if (regexp[1] == '*') {
return matchstar(regexp[0], regexp+2, text);
}
if (text[0] != '\\0' && (regexp[0] == '.' || regexp[0] == text[0])) {
return matchhere(regexp+1, text+1);
}
return 0;
}
NFA正規表現サブセットの実装例(cont.2)
/* c*regexpパターンをgreedy検索 */
int matchstar(int c, const char *regexp, const char *text)
{
const char *t;
for (t = text; *t != '\\0' && (*t == c || c == '.'); t++) {
; /* キャラクタcのマッチで行けるところまで行く */
}
do { /* バックトラック: 'c*'の後続の正規表現のマッチをバックトラックして検索 */
if (matchhere(regexp, t)) {
return 1;
}
} while (t-- > text);
return 0;
}
NFA正規表現サブセットの実装例(cont.3)
cf.
/* c*regexpパターンの非greedy検索 */
int matchstar(int c, const char *regexp, const char *text)
{
do {
if (matchhere(regexp, text)) {
return 1;
}
} while (text[0] != '\\0' && (*text++ == c || c == '.'));
return 0;
}
7. DFA正規表現のメカニズム
DFA正規表現のメカニズム
NFAとDFAの形式論
- DFA(Deterministic Finite Automaton)
- 決定性有限オートマトン
- 有限オートマトン
- 状態数が有限。入力と状態に応じて状態遷移する
- オートマトンによって定義される言語
- オートマトンが受理する入力記号列の集合
NFAもDFAもどちらも正規表現を認識可能。
NFAとDFAの形式論(cont.)
- NFA(非決定性有限オートマトン)
- ある状態から、ある入力で複数の状態へ遷移可能
- DFA(決定性有限オートマトン)
- ある状態から、ある入力で遷移可能な状態はひとつまたは存在しない
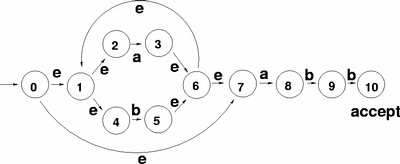
NFAからDFAへの変換
- 開始からε遷移で遷移できる状態集合を求める
- A = { 0, 1, 2, 4, 7 }
- 状態集合Aから入力aとε遷移で遷移できる状態集合を求める
- B = { 1, 2, 3, 4, 6, 7, 8 }
- 状態集合Aから入力bとε遷移で遷移できる状態集合を求める
- C = { 1, 2, 4, 5, 6, 7 }
- 状態集合Bから入力aとε遷移で遷移できる状態集合を求める
- { 1, 2, 3, 4, 6, 7, 8 } => Bと同じ
- 状態集合Bから入力bとε遷移で遷移できる状態集合を求める
- D = { 1, 2, 4, 5, 6, 7, 9 }
- 状態集合Cから入力aとε遷移で遷移できる状態集合を求める
- { 1, 2, 3, 4, 6, 7, 8 } => Bと同じ
- 状態集合Cから入力bとε遷移で遷移できる状態集合を求める
- { 1, 2, 4, 5, 6, 7 } => Cと同じ
- 状態集合Dから入力aとε遷移で遷移できる状態集合を求める
- { 1, 2, 3, 4, 6, 7, 8 } => Bと同じ
- 状態集合Dから入力bとε遷移で遷移できる状態集合を求める
- E = { 1, 2, 4, 5, 6, 7, 10 }
- 状態集合Eから入力aとε遷移で遷移できる状態集合を求める
- { 1, 2, 3, 4, 6, 7, 8 } => Bと同じ
- 状態集合Eから入力bとε遷移で遷移できる状態集合を求める
- { 1, 2, 4, 5, 6, 7 } => Cと同じ
すべてのNFAの状態を尽くすまで続ける
NFAからDFAへの変換(cont.)
正規表現: (a|b)*abb の結果
- A = { 0, 1, 2, 4, 7 }
- B = { 1, 2, 3, 4, 6, 7, 8 }
- C = { 1, 2, 4, 5, 6, 7 }
- D = { 1, 2, 4, 5, 6, 7, 9 }
- E = { 1, 2, 4, 5, 6, 7, 10 }
| 状態 | a | b |
| A | B | C |
| B | B | D |
| C | B | C |
| D | B | E |
| E | B | C |
受理10のあるEが受理
8. NFA vs. DFA
NFA vs. DFA
NFAとDFAの現実
- 本だけ読んでいると、DFAの方が恰好良い
- DFAはNFAより速い (*)
- NFAは最悪のケースで指数オーダーの計算量になる
- (*) egrep(DFA)がgrep(NFA)より速いという伝説の根拠
- egrepの方が遅くなる例は作れます。
DFAは事前に計算することで、テキストのサイズに対してNFAよりスケールする。
NFAとDFAの現実(cont.)
ほとんどのツールはNFA。
- NFA
- perl, python, ruby, tcl, emacs, sed, vi
- DFA
- awk, lex, egrep
- ハイブリッド(前方参照が不要ならDFA、必要ならNFA)
- GNU grep
NFAとDFAの現実(cont.2)
理由(予想)
- NFAの方が融通が効く(前方参照など)
- 実装上のチューニングなどで、NFAでも現実的にはそれなりに動いてしまう
- 正規表現を工夫する手間を人間に押しつけることで、NFAでも現実的にはそれなりに動いてしまう
最後はUnixっぽいかも。
もちろん、勝ち負けの世界ではありません。